

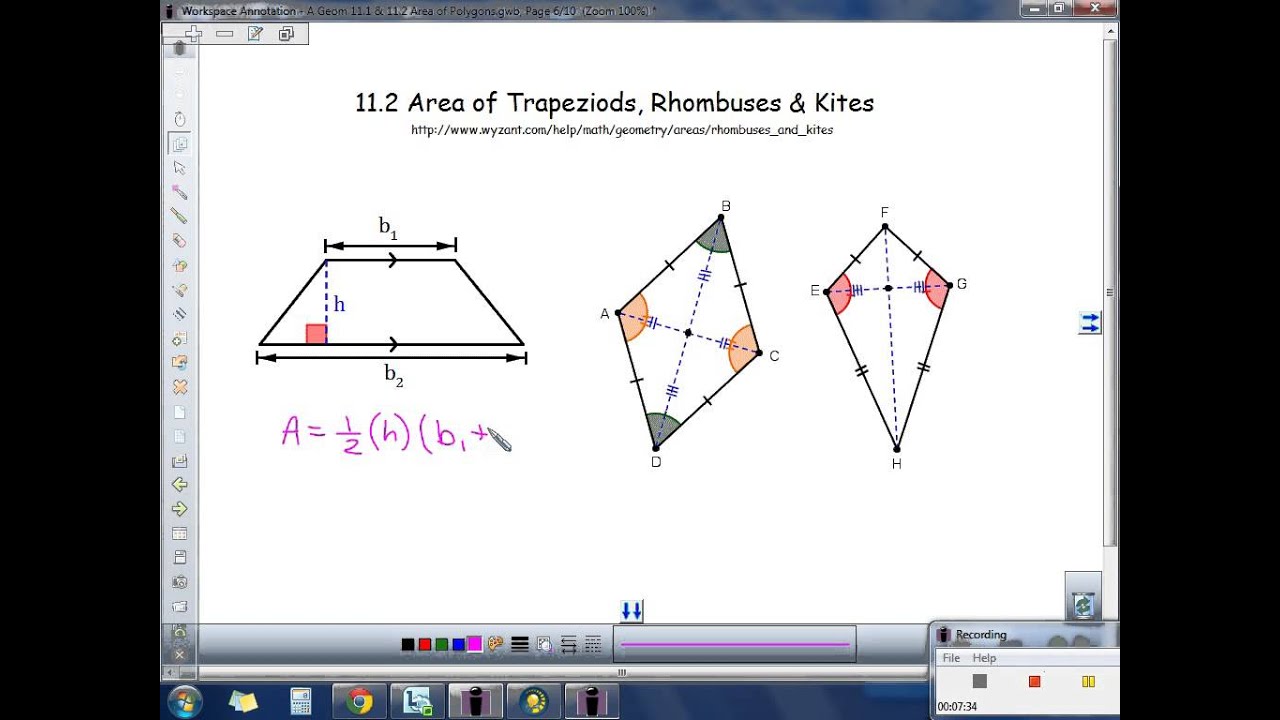
The area A of the triangle is bh = (1)(2) = 1. Draw a segment from S perpendicular to UT. Check Skills You’ll Need 10-2ġ.A = bh 2.A = bh 3. Find the area of each trapezoid by using the formulas for area of a rectangle and area of a triangle. Areas of Trapezoids, Rhombuses, and Kites Lesson 10-2 Check Skills You’ll Need (For help, go to Lesson 10-1.) Write the formula for the area of each type of figure.
#AREAS OF TRAPEZOIDS RHOMBUSES AND KITES PLUS#
6 plus 2 is 8, times 3 isĢ4, divided by 2 is 12. The areas of the small and the large rectangle. Like this that is exactly halfway in between Something like that, and you're multiplying That looks something like- let me do this in orange. Take the average of the two base lengths andĪnother interesting way to think about it. Let's just add up the two base lengths, multiply that times the The bases times the height and then take the average. Ways to think about it- 6 plus 2 over 2, and Then all of that over 2, which is the same Think of it as this is the same thing as 6 plus 2. The height, and then you could take the average of them. So when you think aboutĪn area of a trapezoid, you look at the two bases, the It's going to be 6 times 3 plusĢ times 3, all of that over 2.
Halfway between the areas of the smaller rectangleĪnd the larger rectangle. Sense that the area of the trapezoid, thisĮntire area right over here, should really just And it gets half theĭifference between the smaller and the larger on The smaller rectangle and the larger one on Of the area, half of the difference between Yellow, the smaller rectangle, it reclaims half The trapezoid, you see that if we start with the Halfway in between, because when you look at theĪrea difference between the two rectangles- and let Now, it looks like theĪrea of the trapezoid should be in between The area of a rectangle that has a width of 2Īnd a height of 3. We went with 2 times 3? Well, now we'd be finding Now, the trapezoid isĬlearly less than that, but let's just go with So it would give us thisĮntire area right over there. The area of a figure that looked like- let me do We multiply 6 times 3? Well, that would be the Multiplied this long base 6 times the height 3? So what do we get if Is, given the dimensions that they've given us, what And so this, byĭefinition, is a trapezoid. Where two of the sides are parallel to each other. Either way, you will get the same answer. You can intuitively visualise Steps 1-3 or you can even derive this expression by considering each Area portion and summing up the parts.


Therefore, the area of the Trapezoid is equal to. In Area 3, the triangle area part of the Trapezoid is exactly one half of Area 3 Adding the 2 areas leads to double counting, so we take one half of the sum of smaller rectangle and Area 2ģ. In Area 2, the rectangle area part of the Trapezoid is equal to Area 2 as well as the area of the smaller rectangle. In Area 1, the triangle area part of the Trapezoid is exactly one half of Area 1Ģ. Let's call them Area 1, Area 2 and Area 3 from left to right. Think of it this way - split the larger rectangle into 3 parts as Sal has done in the video. So what Sal means by average in this particular video is that the area of the Trapezoid should be exactly half the area of the larger rectangle (6x3) and the smaller rectangle (2x3).


 0 kommentar(er)
0 kommentar(er)
